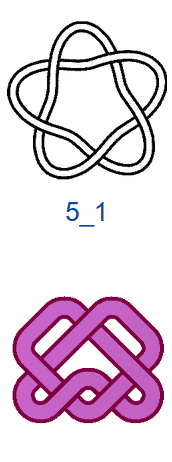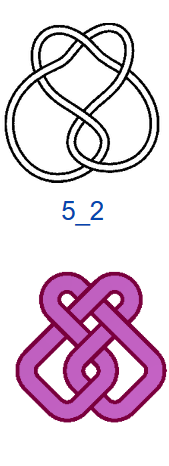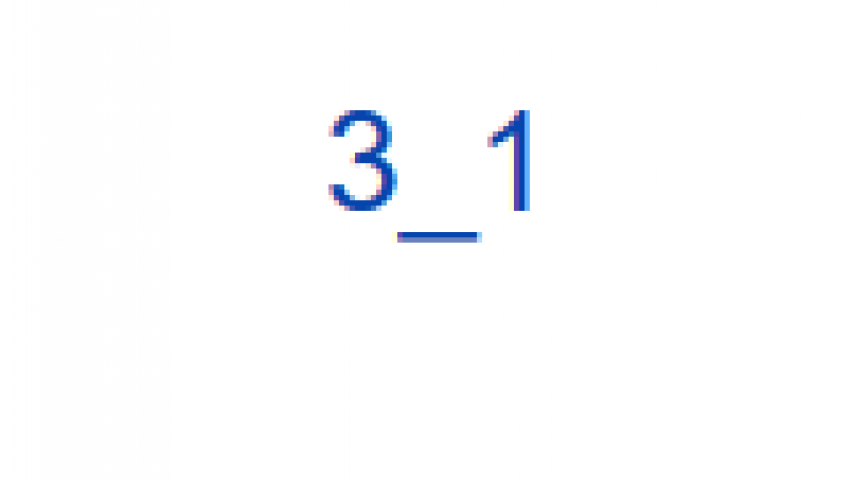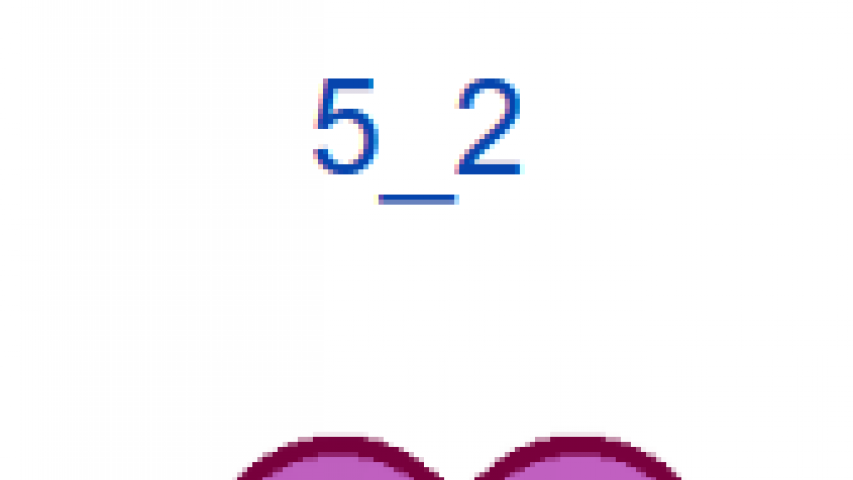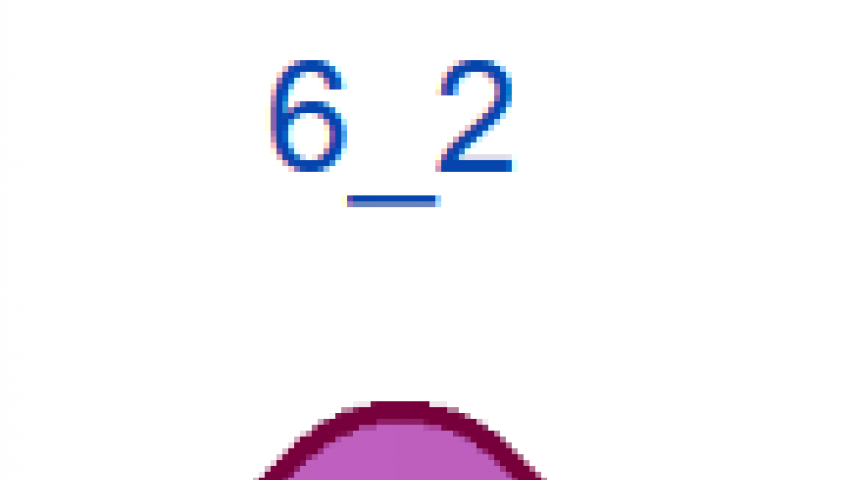Application of the Knot Theory to the Mongolian Knot Design

Введение

С узлами мы знакомимся в детстве, когда нас учат завязывать шнурки, заплетать косички и делать банты. Мама показывает, как завязать узелок на нитке, а папа — как привязать к леске рыболовный крючок. Так мы понимаем, что узлы незаменимы в хозяйственной деятельности. Там, где используется веревка, нитка, канат, — там с древнейших времён применяются разнообразные узлы и техники плетения. Существует множество китайских узлов, гордиев узел, кельтские узлы, морские узлы... Многие из них не только практичны, но и красивы, и именно они, перенесенные на бумагу, используются в графическом дизайне. Современные компьютерные технологии позволяют не только изучать и повторять существующие образцы плетёных узоров, но и создавать новые в соответствии с заданным стилем.

О программе автоматизированной генерации и редактирования плетёнок MonPlet

Для создания плетёнок в монгольском стиле разработан редактор и генератор MonPlet [1]. В принятой в программе математической модели две половины орнамента считаются симметричными, несмотря на различия в переплетениях. Чересстрочные переплетения расставляются программой автоматически. В режиме Редактора предоставляется возможность отрисовки узоров как замкнутых, так и разомкнутых, т.е. фактически можно повторить все примеры из литературы, а также создать множество своих вариантов. При этом с помощью четырех осей симметрии можно симметрировать (копировать по правилам осевой симметрии) части узоров, быстро получая различные образцы. При автоматической генерации плетёных узоров создаются все математически возможные стилизованные монгольские узоры. Из них для графического дизайна и воспроизведения в материале необходимо выбирать наиболее красивые и оригинальные. В программе имеется возможность изменять художественное оформление плетёнки — расстояние между лентами, ширину и толщину ленты и окантовки, радиус поворота ленты, цвет фона, ленты и окантовки.

Классификация традиционных плетеных орнаментов

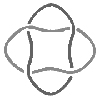
У монголов и бурят — родственных кочевых народов — общий язык, сходные, во многом идентичные обычаи и традиции. Плетение и особые узлы у этих народов употребляются до настоящего времени при изготовлении конской сбруи, плёток, для отделки предметов традиционного костюма, создания наверший для головных уборов, пуговиц. Плетёными орнаментами декорируют двери юрт, мебель, разнообразные бытовые предметы, ювелирные изделия. Самый известный из этих узлов — «вечный узел» («улдзий» по-монгольски или «улзы» по-бурятски), является одним из восьми символов буддизма. Это замкнутая плетёнка из одной ленты, следуя вдоль которой, невозможно найти ни начала, ни конца. Этот знак символизирует вечную жизнь, служит пожеланием бесконечного мира и счастья.

Бурятские и монгольские плетёные узоры во многом схожи, они выполнены в едином стиле, который для краткости назовём монгольским. Характерными чертами этого стиля является квадратная решетка, лежащая в основе построения плетёных узоров, плавные (по дуге окружности) или прямоугольные изгибы лент, и наличие в узоре хотя бы одной из возможных симметрий: зеркальной (m) или поворотной (n).

Передаваемые из поколения в поколение образцы монгольских плетёных розеток (обособленных узоров) опубликованы в книгах Л. Батчулууна [2, с. 255–260] и Ц. Ядамжава [3, с. 52–56], традиционные бурятские плетёнки — в альбоме Л. Доржиева [4, с. 23, 52, 56, 59 и др.]. Всего нами рассматривалось более двухсот образцов народных узоров, из которых были исключены орнаменты, построенные на неравномерной сетке или имеющие другие отклонения от вышеназванных условий. В результате осталось 179 плетёнок, которые были проанализированы более полно.

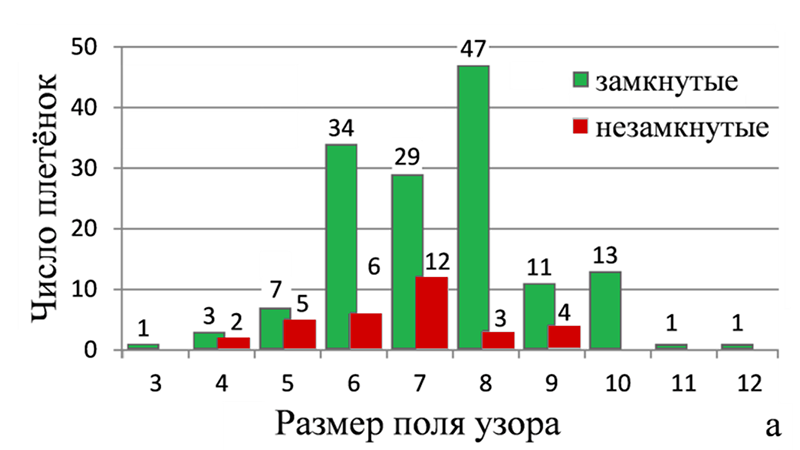
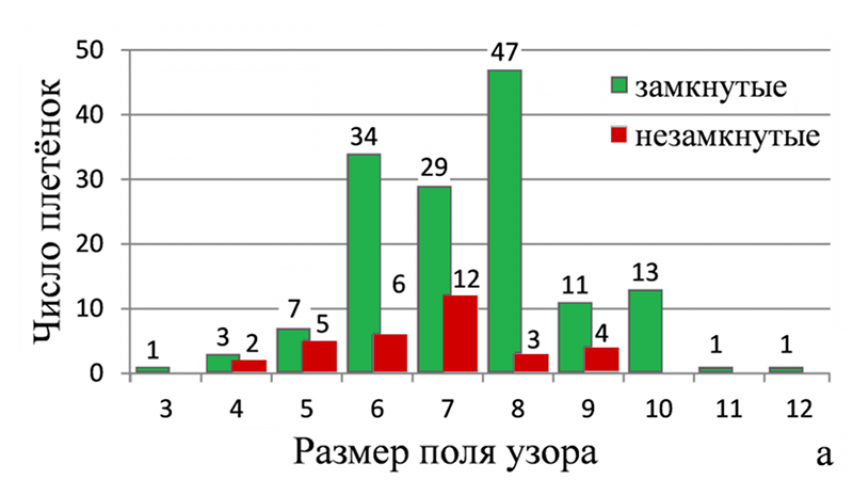
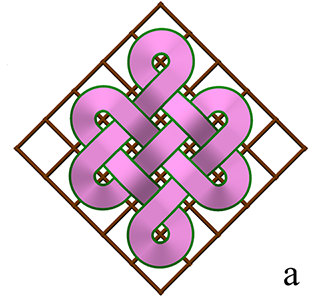
Нужно отметить, что для рисования плетёных узоров художнику необходимо использовать чертёжные инструменты — линейку, циркуль. Мастер должен быть очень внимательным, чтобы не ошибиться в порядке переплетения лент, в соблюдении размеров и симметрии. Чем больше размер сетки-основы, тем больше вариантов плетёнок можно нарисовать, и тем эта задача сложнее. Наверное, поэтому большинство традиционных узоров вписывается в поля от 6х6 до 8х8 клеток («улзы» строится в поле 5х5 клеток). Эти орнаменты достаточно просты, но и красивы. В больших полях рисование плетёнок вручную более трудоёмко, поэтому, вероятно, число таких образцов не столь велико (рис. 1а).

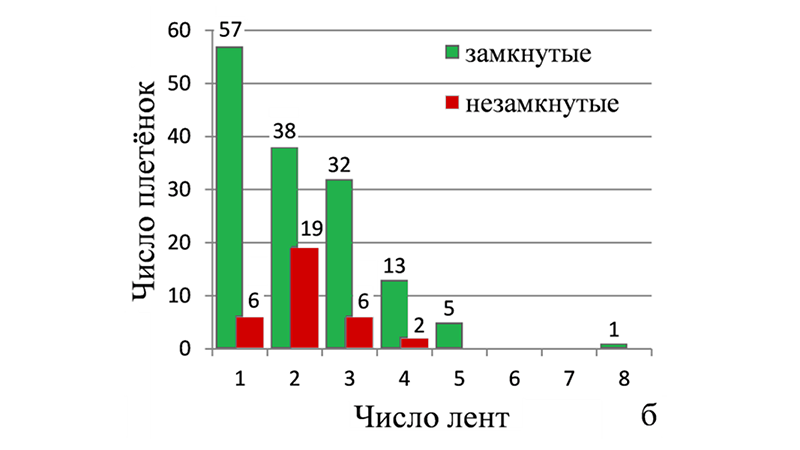
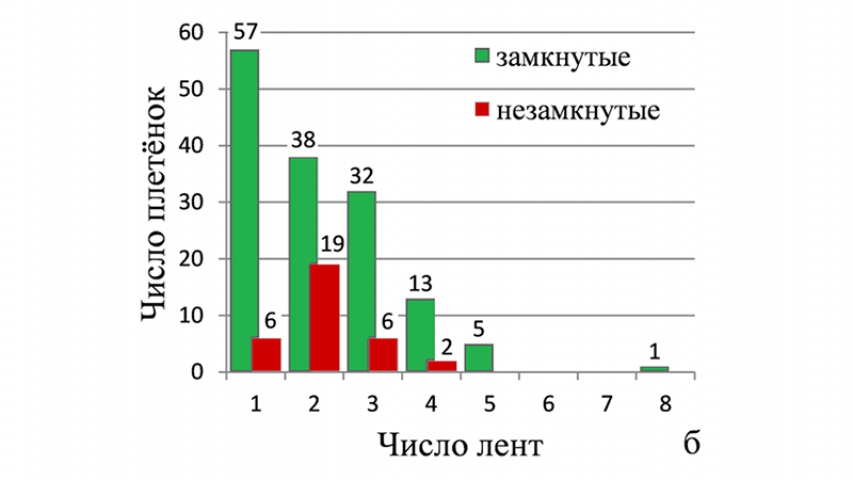
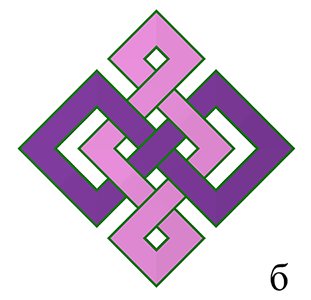
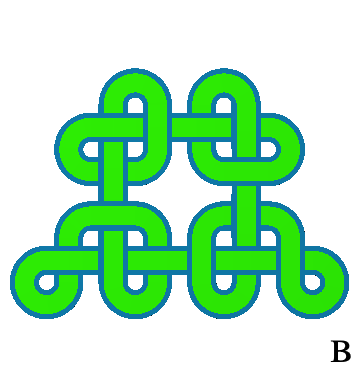
В процессе оцифровки и систематизации этих орнаментов было установлено, что большинство плетёнок состоит из одной замкнутой ленты, а более восьми лент в образцах не встречается (рис. 1б), т.е. с точки зрения математики большинство монгольских плетёных узоров являются узлами.

Элементы теории узлов в приложении к плетёнкам

Узлы интересуют не только дизайнеров и искусствоведов, но и математиков, и теория узлов пытается объяснять и прогнозировать различные свойства этих математических объектов, необходимых для понимания природы топологии и геометрии в трехмерном пространстве. «Узлом» в математике называют замкнутую кусочно-линейную кривую в трехмерном Евклидовом пространстве R3. Узлы, состоящие из двух и более сплетённых окружностей, называют «зацеплениями». Таким образом, замкнутые плетёные орнаменты в терминах теории узлов представляют собой узлы и зацепления. На рис. 2 показаны примеры монгольских плетёнок из разного числа лент.

Узлы в общем представлении — это трёхмерные объекты, а плетёные узоры — условно-трёхмерные, так как переплетения лент занимают небольшой объем, и узор наблюдается с одной, а часто бывает одинаковым с двух сторон. Для сравнения между собой узлов (выявления их эквивалентности) принято рассматривать проекции узлов на плоскость XOY, или их плоские диаграммы. Плоскость выбирают таким образом, чтобы на проекции получалась гладкая кривая с несколькими точками самопересечения, где в каждой точке пересекаются две ветви этой кривой. При этом в каждой точке пересечения одна из ветвей проходит выше (то есть имеет большую координату z), а другая — ниже. Нижняя ветвь на рисунках часто изображается с разрывом, а верхняя — сплошной линией. В плетёных узорах точки пересечения точно зафиксированы сеткой, и ленты пересекаются только под прямыми углами. Если мы будем рассматривать плетёнки как плоские диаграммы, мы сможем лучше изучить их математическую природу.

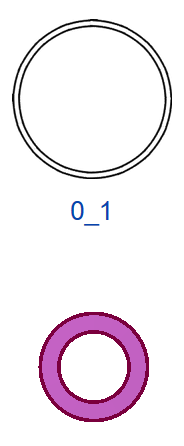
Узлы классифицируют по понятию сложности. Простейший (незапутанный) узел, где число пересечений N=0, называют тривиальным (рис. 3а). Среди монгольских плетёнок имеются образцы, казалось бы, с множеством пересечений, которые, однако, изотопны тривиальному узлу, т.е. их можно распутать (Рис. 3, б–д), используя первое движение Рейдемейстера [5, с. 124]. Узлы изотопны, если один из них можно непрерывно продеформировать в другой [5, с. 122]. Вопрос об изотопии двух узлов — главный в теории узлов. Этот вопрос очень сложен, математики не могут решить его уже более полутора веков. Существующий алгоритм невозможно реализовать на современных компьютерах, однако частные решения оказались чрезвычайно важны и применимы не только в математике, но и в физике, генетике, гидродинамике и других не чисто математических направлениях исследований.

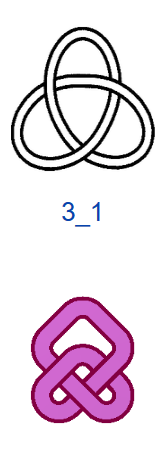
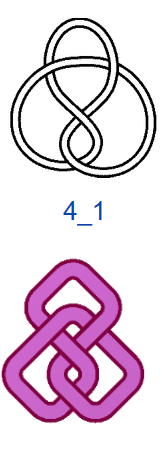
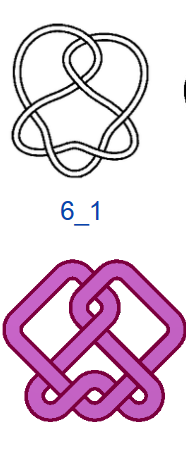
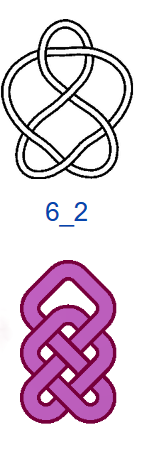
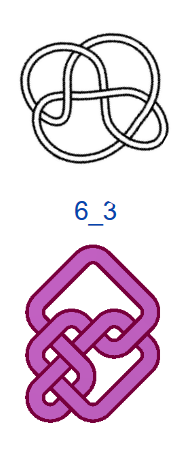
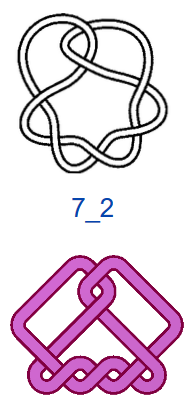
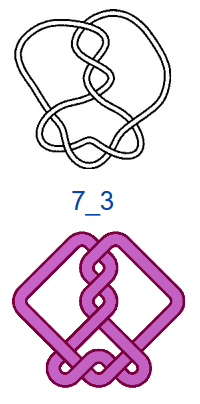
Число самопересечений N, то есть число двойных точек в плоской диаграмме узла, используют в качестве одной из мер сложности узлов. В обозначениях узлов на первом месте ставится число самопересечений N, на втором — порядковый номер узла. Если не рассматривать зеркальные отражения, то существует всего один тип узла, где N=3, — это так называемый «трилистник», и один тип узла с N=4. При N=5 существует два разных узла, а при N=6 — три. При N =7 разных узлов уже семь, и, начиная с этого момента, число типов узлов начинает резко возрастать. При N=13 их уже 12 965, при N=16 — 1 701 935. Не все проекции простых математических узлов обладают симметрией, поэтому число соответствующих им «простых» плетёных узоров будет меньше, чем число узлов, но оно также велико. При этом для узорных плетёнок характерно использование развязываемых петель и различные конфигурации больших петель (>2 клеток), что также увеличивает количество вариаций.

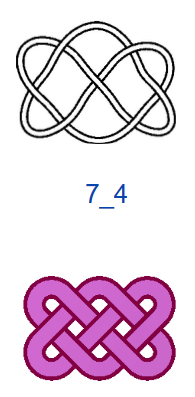
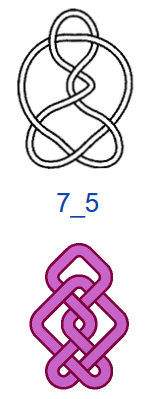
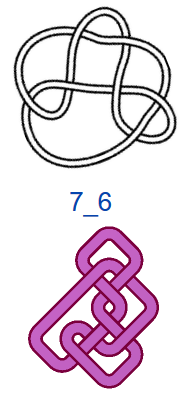
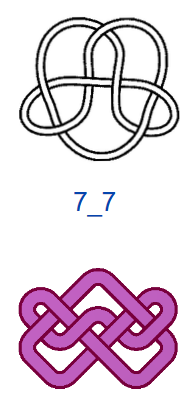
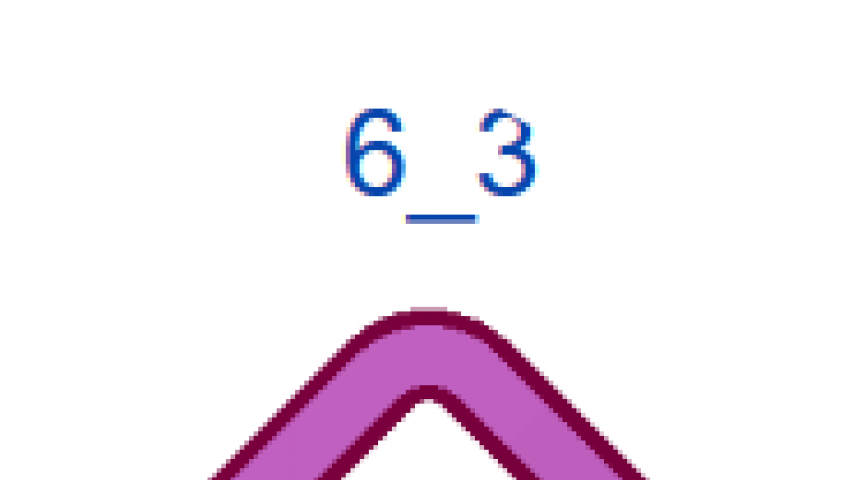
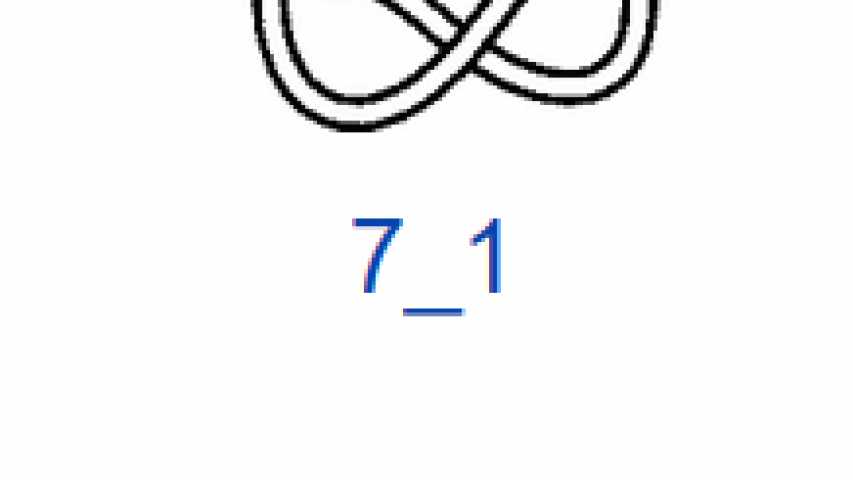
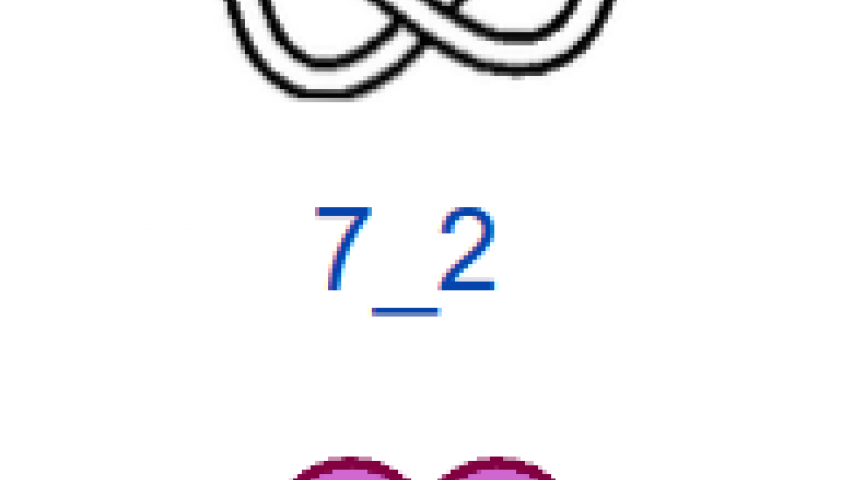
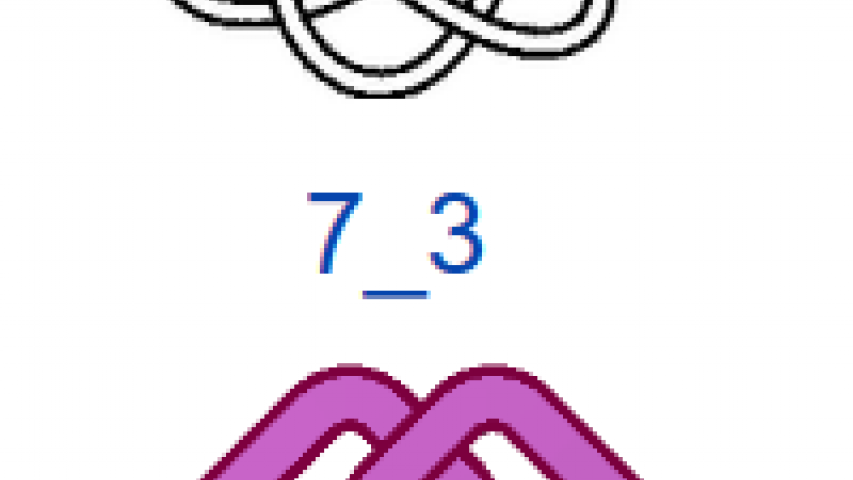
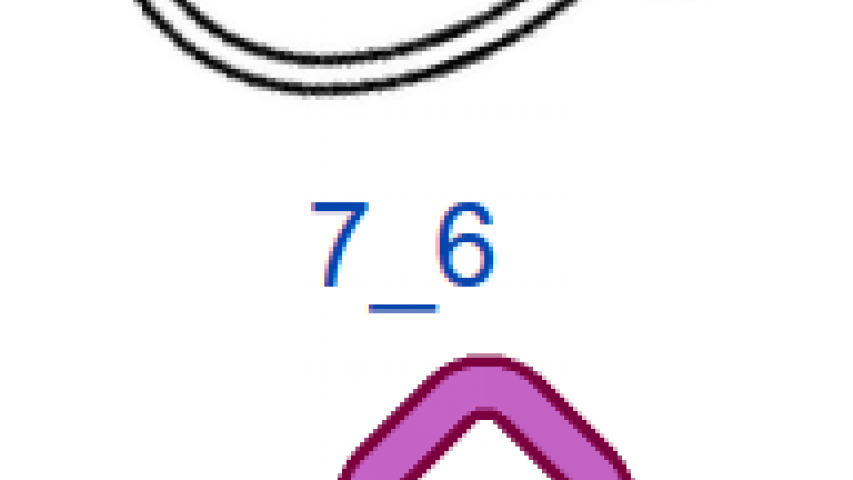
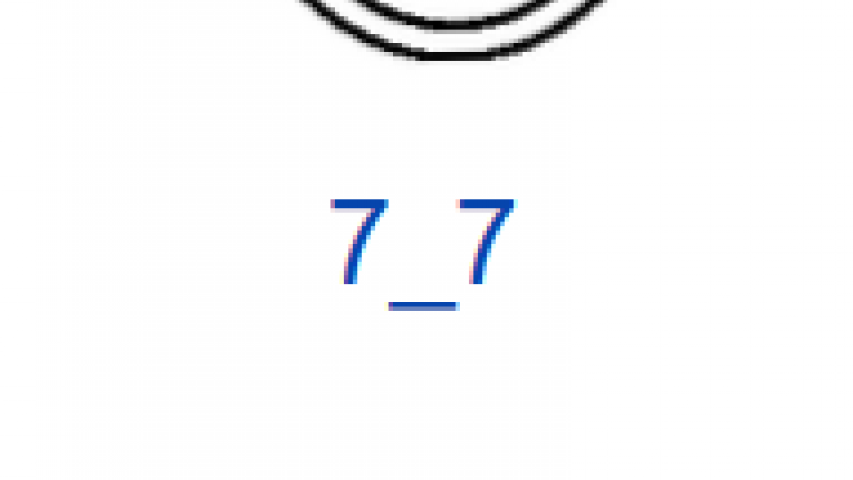
На рис. 4 показаны первые 15 узлов из таблицы простых узлов [6] и соответствующие им примеры простых плетёнок в монгольском стиле. «Простые» они потому, что созданы из характерных петель наименьшей возможной величины (с учётом решетки), т.е. имеют минимальную длину ленты. Из рисунка видно, что плетёнки к узлам 6_3 и 7_6 не обладают какой-либо симметрией, а остальные имеют по одной зеркально-поворотной оси симметрии, кроме узла 7_4, который и есть «вечный узел», если добавить две развязываемые петли к средним петлям. Этот узел обладает двойной зеркально-поворотной симметрией. Кроме него среди литературных образцов имеется ещё только одна плетёнка — аналогичная узлу 6_2. Трилистник встречается в монгольских узлах как симметрируемая часть узора или в преобразованном виде как, например, показано в табл. 1, где рассмотрены замкнутые образцы литературных плетёнок (всего их 12), построенные в малых полях — от 3х3 до 5х5 клеток, в сравнении с простыми узлами. Развязываемые петли придают узлам своеобразие и эстетическую привлекательность, преобразуя их в плетёный орнамент, но при сравнении плетёнок с простыми узлами этими петлями необходимо пренебрегать.

Таблица 1. Монгольские образцы узоров в малых полях, в соответствии с простыми узлами и зацеплениями

Размер поля узора, клетки	3х3	4х4		5х5
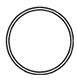
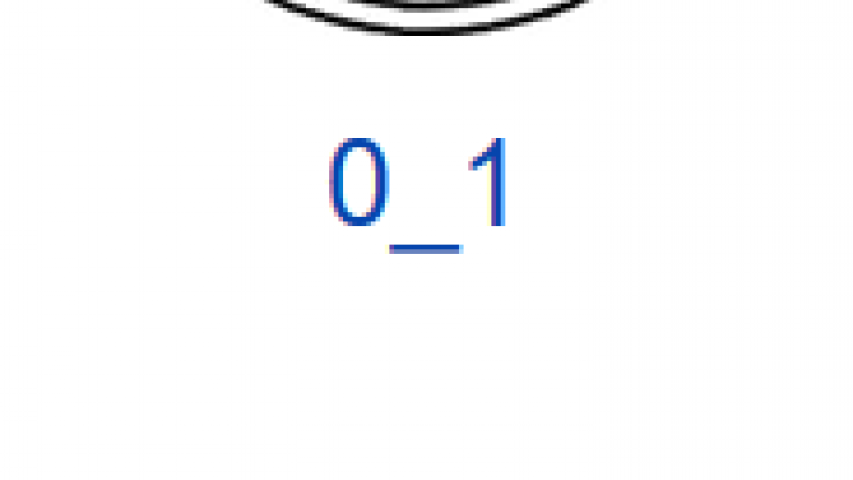
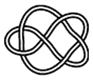
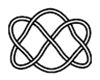
Вид простого узла	0_1			3_1	6_2	7_4
Образец узора
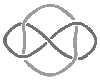
Вид зацепления	–	421			521
Образец узора	–

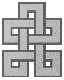Число двойных точек в образцах плетёнок, заполняющих всё поле, построенных в поле 6х6 клеток, достигает 16, 7х7 — 25, 8х8 — 36, 9х9 – 49, 10х10 — 64, т.е. числа достаточно большие. При этом в нечетных полях плетёнки чаще образуются из одной ленты, а в четных — из нескольких звеньев. На данный момент таблицы простых узлов построены до 16 пересечений, зацеплений — до N=9. Но здесь необходимо отметить то, что в плетёнках симметрируемые части узора повторяются от двух до четырех раз, т.е. узлы и зацепления могут умножаться (следовать одно за другим), кратно увеличивая число точек пересечений. Например, на рис. 5 показаны примеры плетёнок на основе трилистника (а–г — имеются в образцах, д — создан в программе MonPlet. В примерах рис. 5 (а, в) добавляются петли по первому движению Рейдемейстера, в образцах (б–д) используется умножение (симметрирование) узлов.

Заключение

Одним из путей оптимизации работы генератора монгольских плетёнок MonPlet может быть применение классификации монгольских плетёных орнаментов (МПО) с помощью элементов теории узлов. Необходимо проанализировать все варианты образцов плетёнок, начиная с малых полей и выделяя те, что представляют собой простые узлы и зацепления, построенные в данном стиле и имеющие наименьшую длину. Составив, таким образом, таблицы простых узлов и зацеплений в стиле МПО и применяя к каждому элементу этих таблиц два простых правила: растяжение отдельных участков для получения стилизованных наружных петель и внутренних пустот и создание дополнительных (развязываемых) пересечений, а также умножение получающихся узлов, можно создать множество вариантов плетёнок в монгольском стиле. Так же могут быть проведены специальные операции — не изменяющие структуру и придающие своеобразие. Это может быть искажение сетки и добавление дополнительных декоративных элементов (растительные завитки, геометрические и зооморфные мотивы, шарф-хадак и т.п.).