Cognitivity in Algorithmization

Введение

Рассматривается логика интуитивных рассуждений (когнитивность), которая лежит в основе алгоритмического мышления, как элемента психологии [1, 2]. К сожалению, в общем образовании это никак не акцентируется, и в программах образования отсутствует общий курс психологии, необходимый для жизни и профессионализма в любой деятельности со средней школы и, тем более, в высшем образовании. Практически все математические теории возникли в когнитивности, и алгоритмическая практика — это алгоритмизация с использованием этих теорий.

Теория алгоритмов ориентируется, как правило, на автоматы-исполнители, манипулирующие знаниями в виде численных данных и текстов [3, 4, 5], что не всегда возможно для различных видов информации, и тогда задача в существующих теориях (Data Science) не решается.

В работе приводится пример логической задачи Л. Кэрролла [6], сформулированной вербально в переводе с английского языка и предлагаемой для интуитивного алгоритмического решения. Используя язык и теорию математической логики [7], задача может быть сведена к ручному алгоритмическому доказательству теоремы или машинной программе в рамках теории.

Второй пример рассматривает историю алгоритмического решения одной из популярных задач Евклида [8], связанной с развитием техники измерений и выбором соответствующих исполнителей алгоритма — в когнитивности интуитивное (ручное) исполнение.

Таким образом, алгоритмическое решение задачи связано с выбором или разработкой некоторой теории в выбранной области знаний и исполнителя, соответственно, преобразованием когнитивного алгоритма в исполнимую запись на языке этой теории. В такой постановке известные в теории алгоритмов [3, 4, 5] машины Тьюринга и Поста, Марковские алгоритмы не эффективны (не универсальны в применении к когнитивным знаниям), так как данные для исполнения должны быть представлены числами, двоичными кодами, текстами.

В алгоритмизации, как в мышлении, знания доступны на естественном языке, расширенном словами из некоторой прикладной области. Задача формулируется как задание в вербальной форме и словарь ограничен только интеллектом разработчика. Для формальной записи алгоритмических рассуждений вербальная запись транслируется в ближайшем и общедоступном языке (например, в графике, в блок-схеме, формулами), применимыми к любому исполнителю. Если алгоритм исполняется компьютером, то необходимы средства ввода для преобразования знаний в данные и средства вывода. Это требует применения алгоритмических языков, включающих необходимые в алгоритмизации определения типов данных, памяти и средств (команд) управления конкретным исполнителем. Алгоритм существенно изменяется и существенно ограничивается его интуитивное восприятие и использование комментариев на вербальном языке алгоритмизации.

Мышление (когниция) определяется в [1, 2] как познавательный процесс, относится к психологии, включает интуитивное накопление и оперирование знаниями, зависит от интеллекта как способности к сохранению, упорядочению и оперативному использованию знаний в жизнедеятельности.

Знания — содержание, смысл воспринимаемых органами чувств внешних объектов (изображение, музыка, речь, ощущения...), сохраняемые в памяти как опыт в формировании новых знаний и алгоритмическом мышлении.

Алгоритмическое мышление ориентировано на решение задач и принятие решений с использованием знаний, формирование новых обобщенных знаний на основе накопленного опыта. Жизнедеятельность человека как процесс определяется алгоритмическим мышлением, включает логику и следующее из нее принятие решения (выполнение некоторых операций). В дальнейшем предполагается когнитивность в алгоритмизации на примерах.

1. Диаграммы мышления

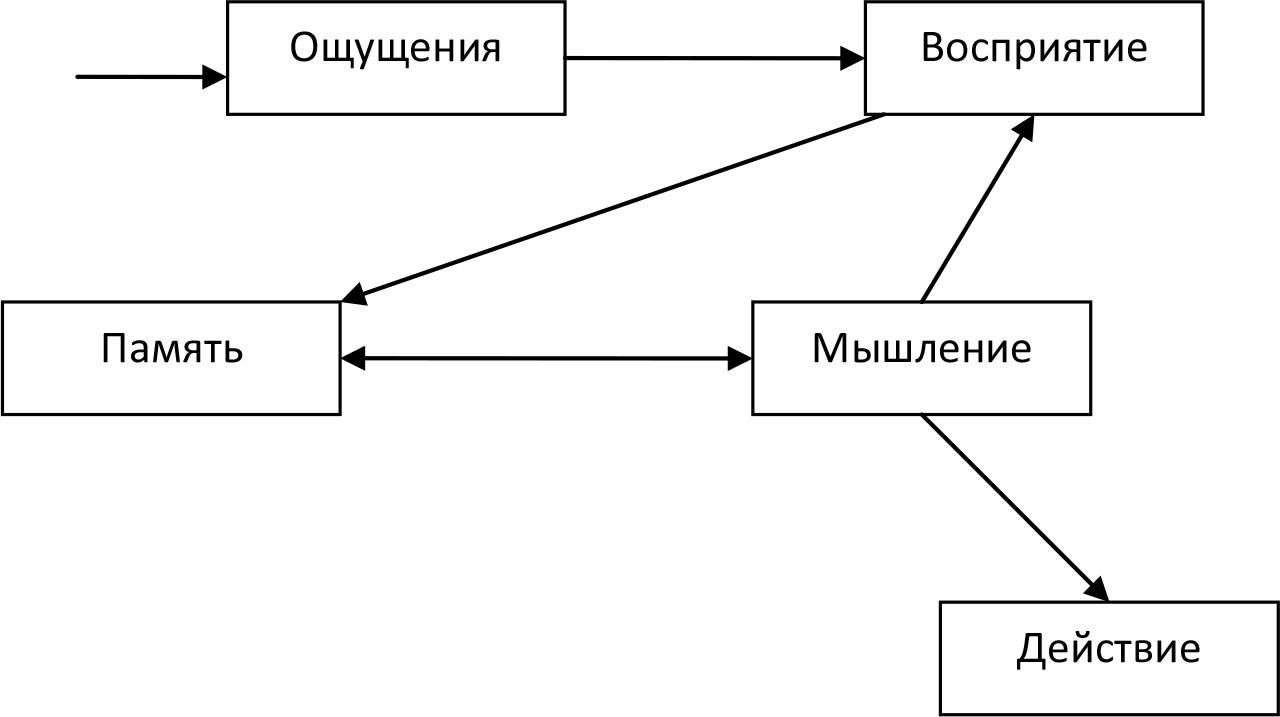
Когниция (cognicio - знание) — познавательная деятельность, в которой фиксируются, обрабатываются в сознании в виде презентаций разные знания. В результате когниции может быть принято решение в виде конкретного действия (Рис. 1).

Когнитивность формирует информационную компетентность и является основой образовательного процесса.

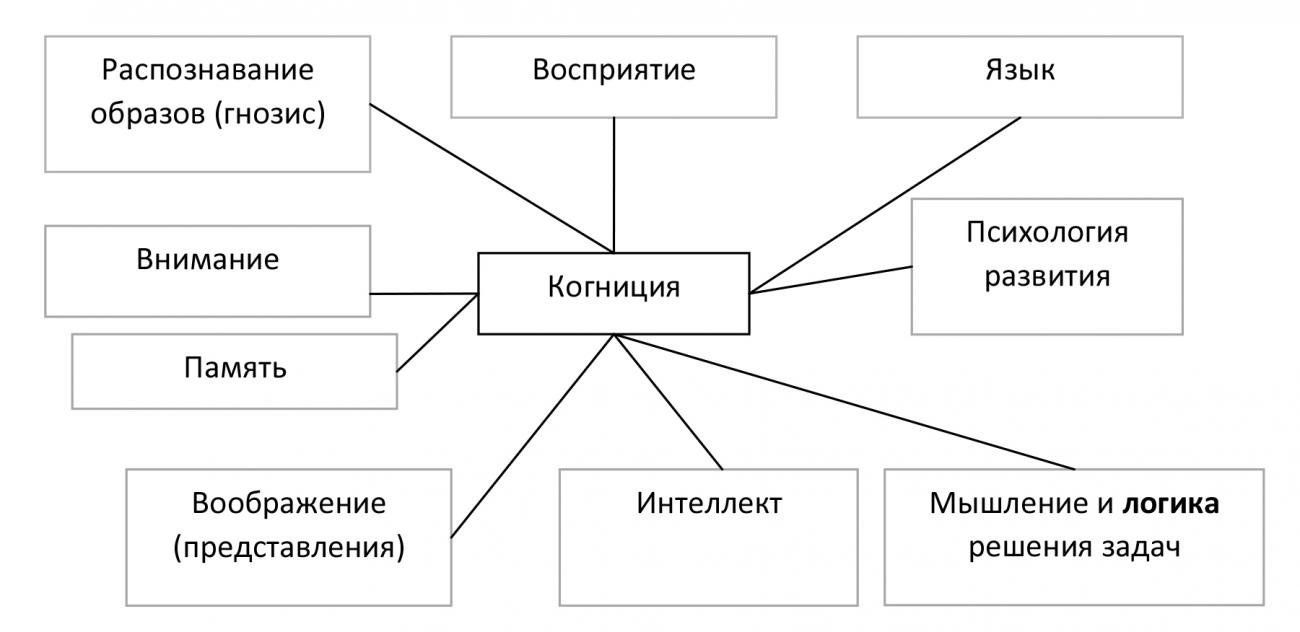
Найссер У. [2] отображает содержание когнитивных процессов, связанных с познанием, более подробной диаграммой (Рис. 2).

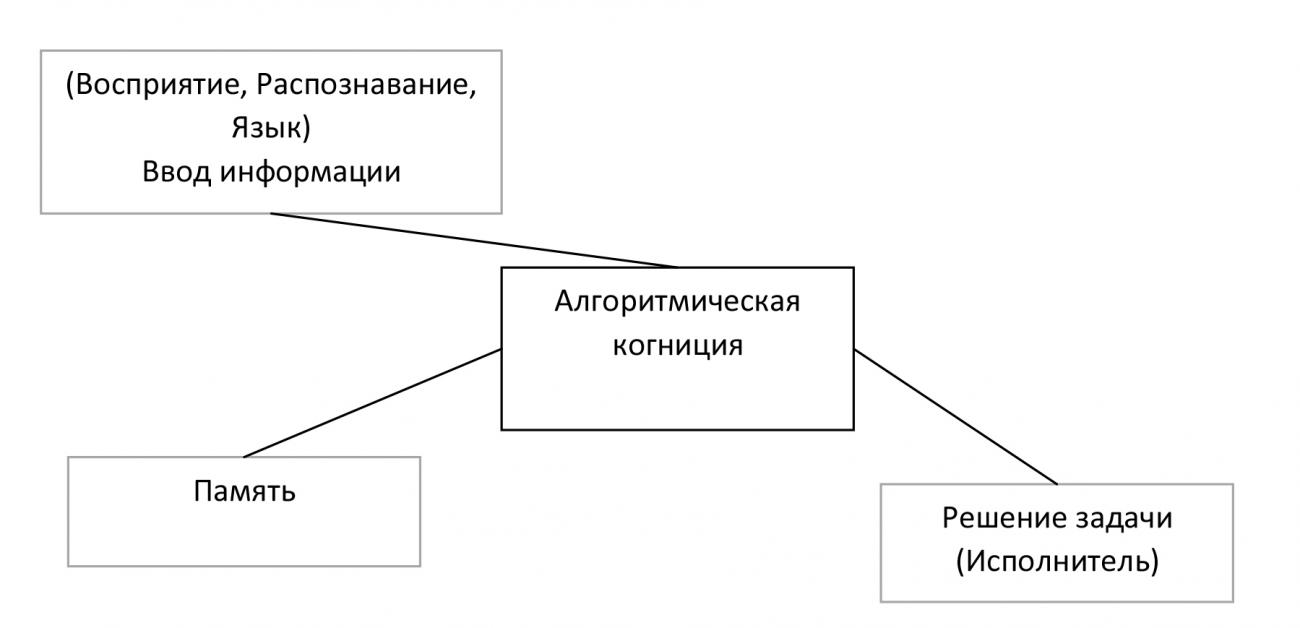
Из диаграммы можно наблюдать сходство с общим интуитивным определением алгоритма [3, 4, 5] и алгоритмическим мышлением, если исключить в диаграмме элементы, имеющее очевидное отношение к психологии (восприятие, внимание, психология развития, интеллект, мышление), и добавить команды, как признаки исполнителя. Получим диаграмму алгоритмизации — процесс создания алгоритма в виде, доступном для исполнения (Рис. 3).

Алгоритмы и алгоритмизация — основополагающие понятия современных образовательных технологий работы со знаниями (информацией) и принятия решений как осознание новой информации (новых знаний). Свойства алгоритмов связаны с конкретными областями знаний и применения алгоритмических технологий. Предполагается участие человека как исполнителя. Для определения этого участия используется понятие алгоритмическое мышление из области психологии.

Алгоритмическое мышление (алгоритмизация) — ввод внешней информации с преобразованием ее в сознании как знания об объективной реальности, сохранение их как опыт, способствуя осознанию и принятию решения (команды исполнителю).

2. Алгоритмизация в математической логике

Алгоритмизация как интуитивный процесс определяет решение некоторой задачи в виде алгоритмического рассуждения, которое может быть записано на естественном языке и формализовано на языке математической логики [5, 7] логическими формулами.

Примеры таких задач представлены для практики в книге Л. Кэрролл [6], рекомендуемой издательством для средней школы.

2.1. Элементы логики

Логику в психологии определяют, как науку о формах и законах мышления в виде истинных рассуждений в процессе познания из полученных ранее истинных знаний или гипотез.

Логика присутствует явно во всех областях жизнедеятельности и определяет порядок выполнения команд исполнителем в алгоритмизации.

Простое высказывание (подлежащее и сказуемое) x — двузначная логическая переменная, значение по умолчанию истинное (x=T).

Инверсия высказывания (x') имеет консенс как существование инверсного по смыслу x высказывания: «Если x=T, то x'=F, иначе если x=F, то x'=T»

В языке математической логики используется обозначение соответствующей алгебраической операции (не x или  ̚  х), где x — двузначная логическая переменная.

Для того, чтобы придать смысл простому высказыванию x, как когнитивному элементу, необходимо осознавать некоторый контекст, в котором переменная x может принимать разные значения.

В математической теории логика рассуждений формализована и представлена формулами булевой алгебры [7].

Обозначение логической операции со смыслом (x И у) ≡ (x ^ у) в составном высказывании позволяет вычислить логический смысл соответствующего составного высказывания. В формулах логики используются также операции: (x ИЛИ у) ≡ (x ˅ у), (x либо у) ≡ (x + у), если x, то у ≡ (x → у), где (→) операция импликации.

Рассуждения в когнитивности могут быть записаны на естественном языке, и, таким образом, переданы для дальнейшей формализации и алгоритмических вычислений в виде формул алгебры логики.

Если формула вида (x → у) является истинной для любых значений истинности x, то элементы предполагаются релевантными (согласованными по смыслу).

При исполнении формулы диссонанс может быть вызван нарушением логики принятия решения и обнаружен при тестировании.

Например, нерелевантное отношение «если завтра не будет дождя (A'), мы пойдем на прогулку (B)», где A' и B по смыслу считаются релевантными и (A' → В) является истинным. Отношение предполагаем релевантным. Однако в рассуждении не учтено, что на следующий день возможен диссонанс («будет дождь» ≡ A) и «необходимо выйти». Рассуждение приводится к консенсу, если уточним утверждение:

C «если завтра не будет дождя (A), мы пойдем на прогулку (B) или пойдем с зонтом (С)» ≡ (A' → В) ˅ (A → С) ≡ В ˅ С ≡  «завтра пойдем, но возьмем с собой зонт на случай дождя».

Формула с учетом интуитивной семантики (смысла конструкций языка) является формальной синтаксической записью интуитивного алгоритма вычисления истинности рассуждений на языке логики, исполняется, по определению дизъюнкции, как истинное при любых значениях A.

Формализация рассуждений в символических формулах теряет смысл и это может приводить при вычислениях и возврату в когнитивной записи к диссонансу, если использовались нерелевантные (несогласованные по смыслу) знания.

Логически правильно построенное вербальное рассуждение гарантирует правильный вывод. Тогда формальное рассуждение, представленное на естественном языке, в математической логике может быть доказано как истинное, что является доказательством правильно построенного (читабельного) когнитивного рассуждения.

2.2. Примеры алгоритмизации в логике предикатов

Рассуждение представлено силлогизмом — две гипотезы и следствие. Требуется найти правильный вывод.

Задача 1.

В применении к высказываниям в задачах Л. Кэрролл [6] — переменные x, y являются аргументами множеств элементов P(x) — множество животных, U(y) — множество моллюсков, простое двузначное высказывание N — несчастный и инверсное (или  ̚  N)— не несчастный:

1. Ни одно животное не может быть несчастным.

2. Моллюск может быть несчастным.

Следовательно, моллюск не животное.

Несмотря на то, что рассуждение логически правильно построено, элементы не согласованы по смыслу (нерелевантные) — свойство может быть или не может быть несчастным “моллюск” относится к психологии человека и вывод является диссонансом.

Задача 2.

Формализация в математической логике позволяет доказать правильность формальной записи правильно логически организованных интуитивных рассуждений безотносительно к когнитивному смыслу. Содержание диаграмм Кэрролла также подтверждают только правильность построения логики рассуждений.

3. Алгоритмизация в измерениях

Задача Евклида [8] — “алгоритм измерения длин отрезков с использованием общей единицы измерения при доступных во времена Евклида простых средств измерения сравнением.

Для вербального описания интуитивного алгоритма измерений необходима некоторая условная текстовая формализация, хотя бы для символических ссылок на упоминаемые длины отрезков.

Когнитивность как процесс решения задачи представляем в виде списка истинных утверждений, обозначающих знания, вопросы, которые последовательно формулируются в сознании, и ответы, определяющие логику выбора альтернативы  для устранения возможного диссонанса.

Рассмотрим интуитивную модель измерений. Графическая интерпретация измерений может быть выполнена геометрическими построениями, например, циркулем и линейкой:

1.  Исходные знания — пара отрезков S_i и S_j — визуально, контролируется S_i≠0, S_j≠0.
2. Контролируется простым совмещением, истинное отношение S_i(>, <, =)S_j. Выбираем одно из альтернативных отношений:
   1. если (S_i>S_j), обозначим разность отрезков S_i = S_i\S_j и возвращаемся к шагу 2.
   2. если (S_i<S_j), обозначим отрезки S_ißàSj, S_j обозначается как S_i и S_i как S_jвозвращаемся к шагу 2.
   3. если (S_i=S_j), следующий шаг — алгоритм завершается.
3. S_i — общая мера.

Интуитивно очевидно, что для истинных отношений шаги 1–2 алгоритма исполняются за конечное время и алгоритм конечный, диссонанс не предсказуем. Задача алгоритмически разрешима и применима к любым исходным, совместимым по доступности измерений Si и Sj.

4. Поиск пути в лабиринте

Задачи игровые популярны для развития мышления. Достоинства их в удобных графических формах задания и демонстрации интуитивного исполнения алгоритма.

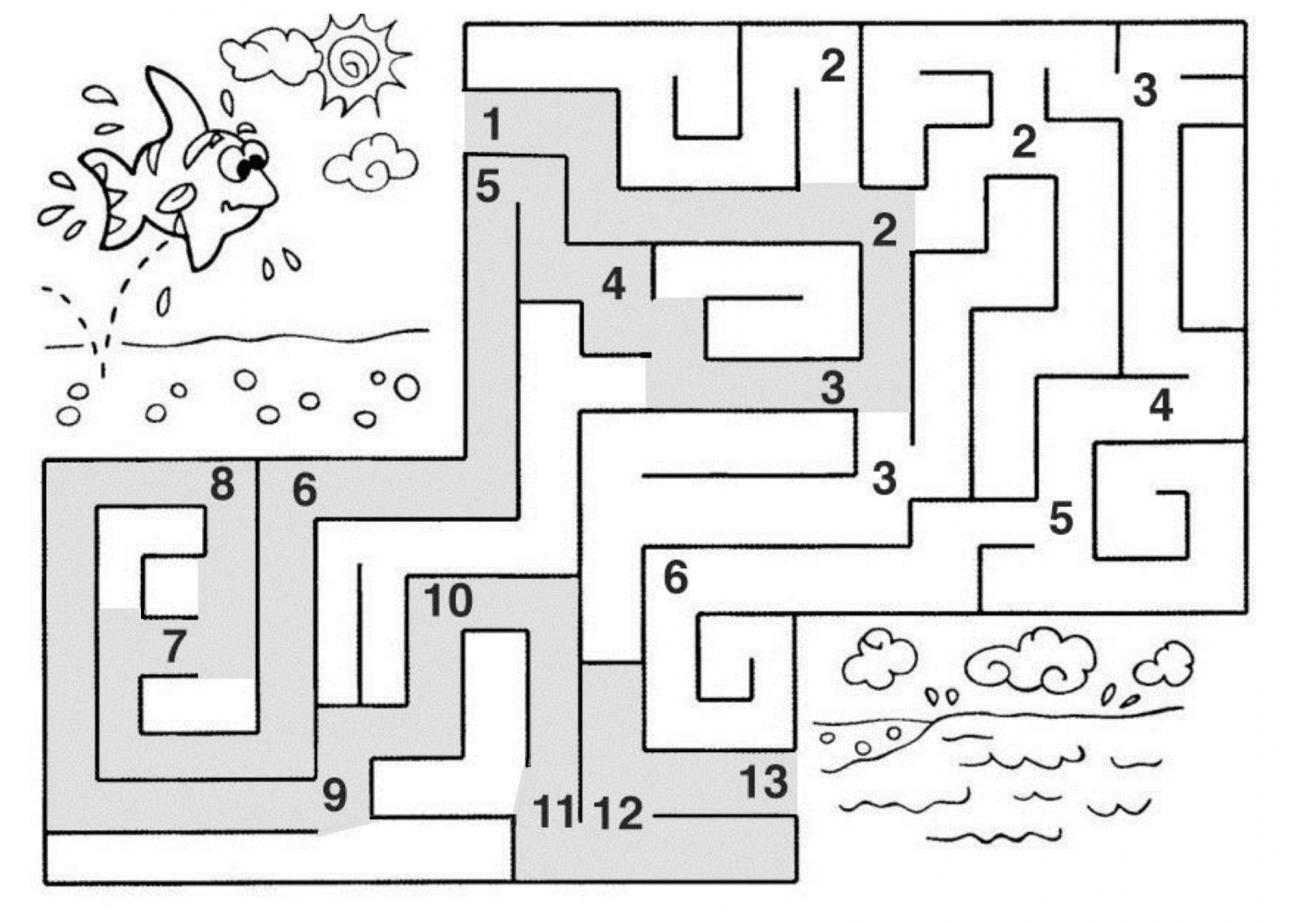
При этом шаги алгоритма наглядны и результаты запоминаются средствами графики. Популярная задача выбора пути в лабиринте. На рис.4 приведена задача поиска пути в бассейне в виде графической диаграммы. Задача должна быть решена алгоритмически — простой случайный перебор не приемлем. Очевидны единственные доступные вход в бассейн и выход.

Предлагается выполнить конечное число простых шагов вручную, например, расстановкой номеров, обозначающих допустимый и визуально контролируемый последовательно идентифицируемый путь. Возможно интуитивное исполнение следующего алгоритма

1. Видимую область диаграммы на входе обозначим N=1.
2. Следующие по порядку области N=N+1 связаны с предыдущими, отмеченными N, если области смежны и доступны в графике без пересечений с линиями.
3. Повторить шаг (2) последовательно до тех пор, пока не достигнута область на выходе бассейна.
4. Таким образом, путь доступа в лабиринте определяет последовательность отмеченных номеров областей бассейна.

На рис. 4 приведено графическое описание форматов данных и преобразований для поддержки когниции — выбраны последовательные номера областей N=1, 2, 3, ...11, 12. Игровая задача имеет только визуально-ручное интуитивное алгоримическое решение. Для программирования потребуется другая численная модель, и это уже принципиально другое решение и алгоритмизация.

Заключение

Алгоритмизация обычно подразумевается в «искусственном интеллекте», где исполнителем является компьютер, и формализация алгоритма представлена в виде программы. При этом знания как данные представлены числами или цифровыми кодами, что подразумевает возможность формального математического описания и решения задачи с прямым использованием блок-схем. Графика позволяет интуитивно контролировать алгоритмизацию, ограничиваясь для проверки программ тестированием. Однако во многих случаях необходимо текстовое или графическое описание форматов данных и преобразований для поддержки когниции.

Развитие науки и техники ставит новые задачи, относящиеся к когнистике. В частности, отношения социальные при создании и эксплуатации приборов и технических систем, биология, химия и другие ограниченно оцифрованные науки и дисциплины так называемого искусственного “интеллекта.

В процесс алгоритмизации интуиция сводит решение задачи к логике шагов исполнителя (команды, процедуры, условия). Процесс индивидуален — от постановки задачи, доступности информации и выбора исполнителя и постоянного контроля согласованной формализации в когнитивности и в алгоритмизации.

В примерах в когниции используется естественный язык для определения необходимых знаний, доступа к ним и формализации, которые позволяют выполнить алгоритмы интуитивно. Интуицию (интеллект) невозможно заменить искусственными устройствами, которые всегда являются исполнителями в одном из способов формализации известного алгоритма и нет гарантии, что будет обнаружен когнитивный диссонанс, если по определению, он не предсказуем.

Алгоритмизация как способ существования затрагивает на практике многие вопросы (например, экономики, политики, медицины), затрагиваемые общим образованием, и не могут быть даже упомянуты в доступном ограниченном объеме статьи. Например, стандартизация  измерений на практике, в науке и экономике.